Low-Precision Training with Multiplicative Weight Update Algorithm Madam
Training deep neural networks consumes extensive energy and generates a large amount of carbon emissions. For example, suggested by this article, training a final version of MegatronLM costs 27,648 kilowatt hours (kWh), which is similar to the energy consumption of three households in the U.S. for a year. Traditionally, values in neural networks are represented using floating-point (32-bit) numbers, which incurs large arithmetic and memory footprint, and hence significant energy consumption. In contrast, low-precision numbers only require low-bitwidth computational units, leading to better computational efficiency and less required memory bandwidth and capacity. To achieve low-precision training, we develop a co-designed low-precision training framework, termed LNS-Madam, in which we jointly design a logarithmic number system (LNS) and a multiplicative weight update algorithm (Madam).
List of Papers
Learning compositional functions via multiplicative weight updates (link)
LNS-Madam: Low-Precision Training in Logarithmic Number System using Multiplicative Weight Update (link)
Madam Optimizer - Multiplicative Weight Update for Deep Learning
Learning compositional functions via gradient descent incurs well known problems like vanishing and exploding gradients, making careful learning rate tuning essential for real-world applications. In contrast to additive learning algorithms such as gradient descent, we propose a multiplicative weight update method Madam - a multiplicative version of the Adam optimizer. Madam updates the weights directly in logarithmic space, such that:
\[W \gets W \odot \exp \left[-\eta\,\mathrm{sign} W \odot\, \left(\frac{g}{\bar{g}}\right)\right]\]where \(\odot\) denotes element-wise multiplication, \(\eta\) is the learning rate, and \(\bar{g}\) represent the normalized gradient.
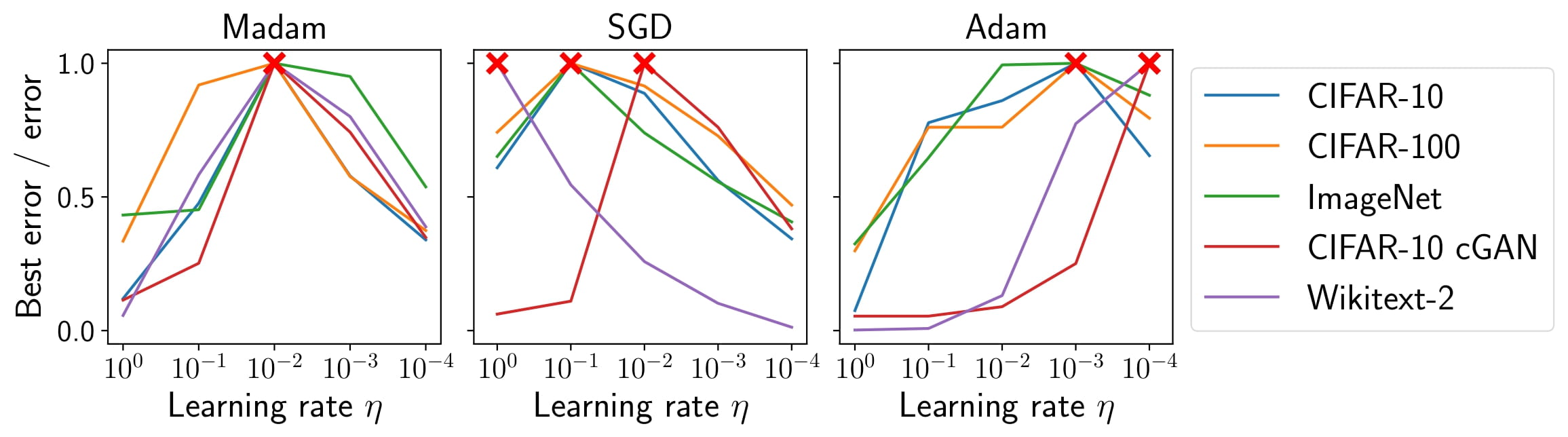
We prove that multiplicative weight updates satisfy a descent lemma tailored to compositional functions. As shown above, our empirical results suggest that Madam can train state-of-the-art neural network architectures without learning rate tuning.
Representing Neural Networks in Logarithmic Number System
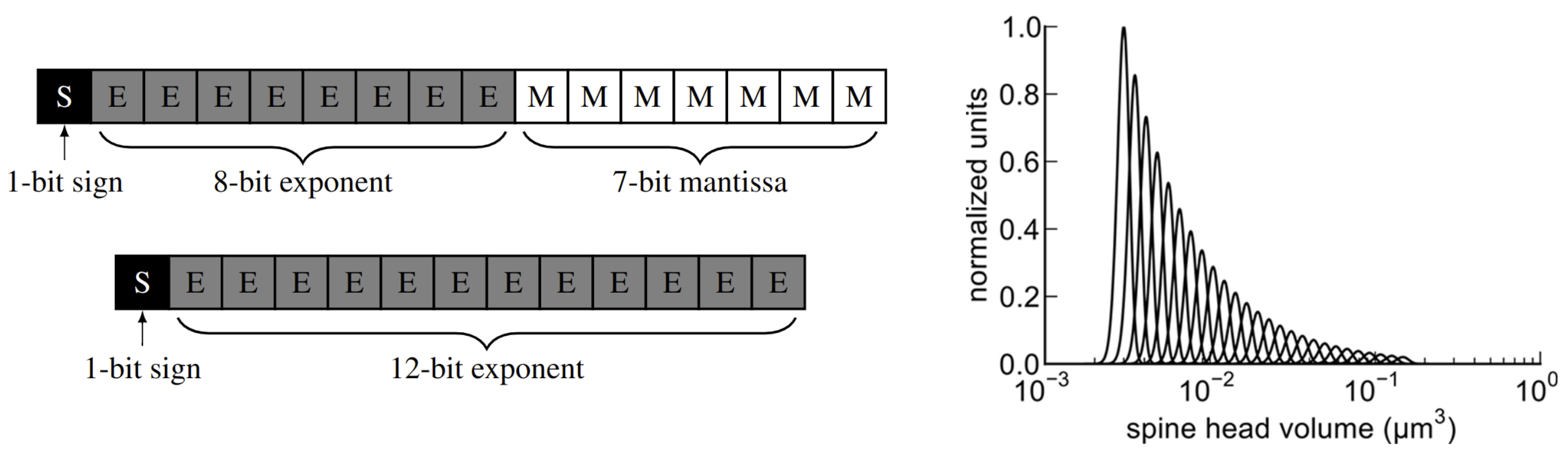
While low-precision training methods generally reduce computational costs, energy efficiency can be further improved by choosing a logarithmic number system (LNS) for representing numbers. As shown in the above figure (left), we compare bfloat16 number system (upper) with a logarithmic number system (lower), where LNS only has sign and exponents. Representing neural networks using LNS is in line with biological findings, suggested by Bartol et al., that the brain may use ``a form of non-uniform quantization which efficiently encodes the dynamic range of synaptic strengths at constant precision’’—or in other words, a logarithmic number system. The above figure (right) is the synaptic distribution suggested by Bartol et al..
In addition, LNS is energy efficient. It achieves a higher computational efficiency by transforming expensive multiplication operations in the network layers to inexpensive additions in their logarithmic representations.
LNS-Madam
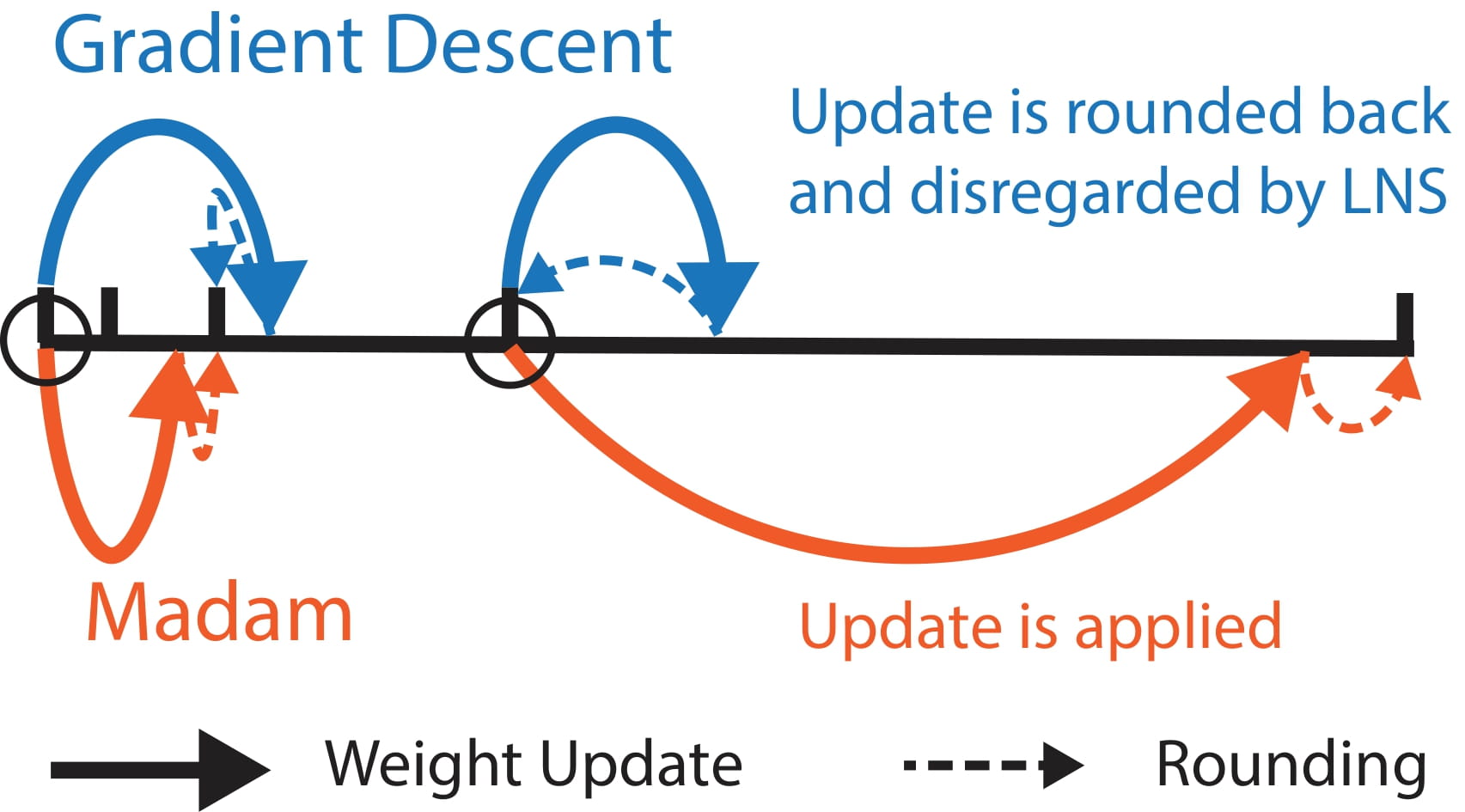
Because Madam optimizer directly updates the weights in the logarithmic space, it is natural to apply Madam over the weights in LNS. As shown above, Madam induces less quantization error compared to gradient descent, as Madam’s updates are scaled with the weight magnitudes accordingly. Motivated by this benefit, we develop a co-designed low-precision training framework LNS-Madam, in which we jointly design the logarithmic number system (LNS) and the multiplicative weight update algorithm Madam.
Results
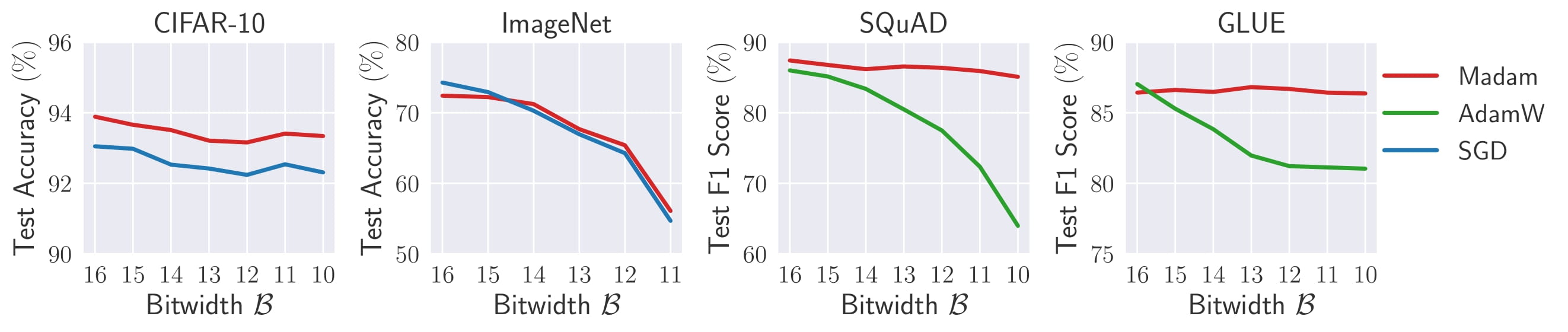
We compare Madam with different optimizers over various datasets and models. As shown above, training with Madam leads to a stable convergence even if precision is strongly limited.
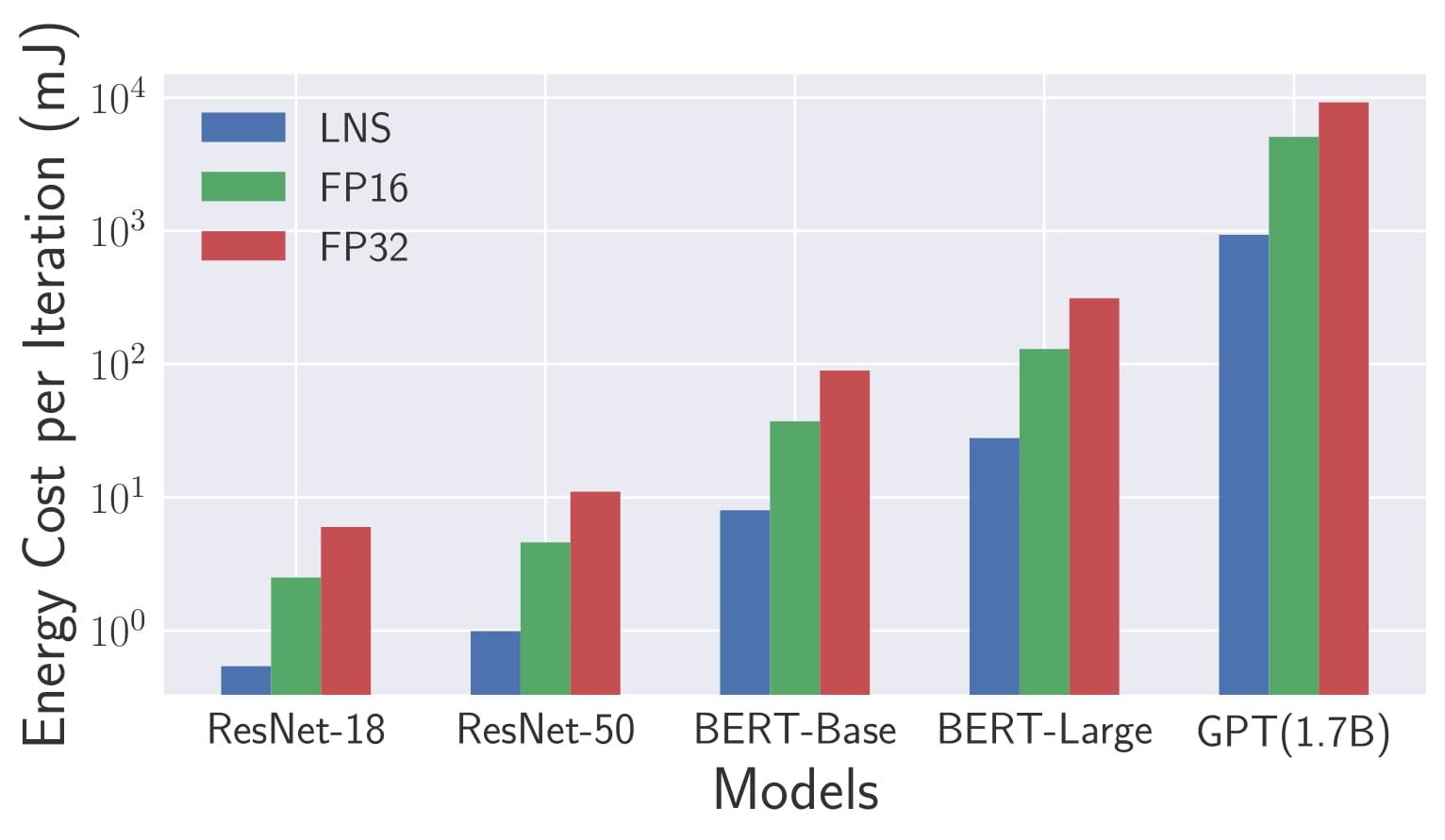
8-bit LNS-Madam also shows great energy efficiency. Compared to a full-precision floating-point implementation, 8-bit LNS-Madam reduces the energy consumption by over 90% while preserving the prediction performance.